Read, Write, and Do Something

No Teaching without learning

Menulislah agar abadi

---

Listen, free economic make better

Showing posts with label Data Analyst. Show all posts
Showing posts with label Data Analyst. Show all posts

26/09/2023

REGRESI BERGANDA DAN MACHINE LEARNING

September 26, 2023  , , ,  No comments

 REGRESI BERGANDA DAN MACHINE LEARNING

Analisis regresi bertujuan untuk memprediksi nilai variable tak bebas, jika variabel bebas diketahui datanya. Persamaan regresi yang memenuhi kriteria BLUE (Best, Linier, Unbiased, Estimated) dapat dijadikan alat prediksi yang baik. Dari laman www.statisticssolutions.com mengemukakan, Three major uses for regression analysis are 

  1. Determining the strength of predictors, 
  2. Forecasting an effect, and 
  3. Trend forecasting 

Persamaan regresi merupakan suatu persamaan yang menerangkan atau menjelaskan hubungan antara variabel bebas dan variabel tak bebas. Persamaan regresi dapat digunakan untuk memprediksi atau mengestimasi nilai dari variabel tak bebas berdasarkan informasi dari variabel bebas. Persamaan regresi linear merupakan suatu persamaan yang berupa garis lurus, sedangkan persamaan regresi nonlinear bukan merupakan persamaan garis lurus.

Model Persamaan Regresi Berganda  :


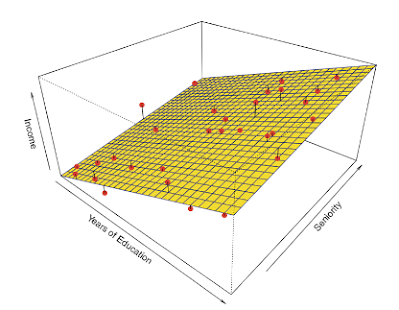
Visualisasi Regresi berganda


Contoh aplikasi dari regresi linear berganda

  • Membuat persamaan untuk memprediksi atau mengestimasi nilai indeks prestasi mahasiswa berdasarkan jumlah jam belajar dalam sehari dan intelligence quotient (IQ). Di samping itu dapat diketahui faktor-faktor yang memberikan kontribusi paling besar dalam hal pengaruhnya terhadap indeks prestasi mahasiswa.
  • Membuat model untuk memprediksi atau mengestimasi laba perusahaan berdasarkan umur perusahaan, tingkat penjualan, dan besarnya perusahaan. Di samping itu, dapat diketahui seberapa besar kontribusi yang diberikan dari faktor umur perusahaan terhadap naik/turunnya laba perusahaan, dengan mengontrol pengaruh tingkat penjualan dan besarnya perusahaan. Dapat juga diketahui seberapa besar kontribusi yang diberikan dari faktor tingkat penjualan perusahaan terhadap naik/turunnya laba perusahaan, dengan mengontrol pengaruh umur perusahaan dan besarnya perusahaan.
  • Membuat persamaan untuk memprediksi atau mengestimasi harga saham suatu perusahaan berdasarkan laba per-lembar saham dan jumlah kas dividen yang diberikan. Di samping itu, dapat diketahui seberapa besar kontribusi yang diberikan dari faktor laba per-lembar saham terhadap naik/turunnya harga saham, dengan mengontrol pengaruh jumlah kas dividen yang diberikan.
  • Pada kasus makro ekonomi, kita dapat megestimasi pertumbuhan ekonomi dengan melihat kontribusi variabel bebas seperti inflasi, pendapatan, suku bunga. dll.

Regresi dan Mechine Learning

Ada berbagai jenis algoritma Machine Learning yang digunakan dalam berbagai aplikasi, seperti algoritma regresi, klasifikasi, clustering, dan deep learning.

Algoritma machine learning adalah sekumpulan aturan yang digunakan oleh sistem machine learning untuk mengambil keputusan atau membuat prediksi. Algoritma dalam machine learning dapat dibagi menjadi tiga kategori yaitu supervised learning, unsupervised learning, Reinforce Learning. 

Supervised learning adalah algoritma yang digunakan untuk membuat prediksi berdasarkan data latihan yang sudah ditandai dengan label atau target yang diinginkan. Sedangkan unsupervised learning adalah algoritma yang digunakan untuk menemukan struktur atau pola dalam data yang tidak dikenal sebelumnya. Ada berbagai jenis algoritma machine learning yang digunakan dalam berbagai aplikasi, seperti algoritma regresi, klasifikasi, clustering, dan deep learning.

Jenis-Jenis Algoritma yang Digunakan dalam Machine Learning
Ada beberapa jenis algoritma yang digunakan dalam machine learning, diantaranya:

  1. Algoritma Regresi: Algoritma ini digunakan untuk memprediksi nilai numerik seperti harga saham, harga properti, atau jumlah penjualan. Algoritma ini digunakan untuk membuat model prediksi yang dapat digunakan untuk membuat keputusan bisnis.
  2. Algoritma Klasifikasi: Algoritma ini digunakan untuk memprediksi kelas suatu objek seperti mengklasifikasikan email sebagai spam atau tidak spam, atau mengklasifikasikan pasien sebagai menderita penyakit tertentu atau tidak. Algoritma ini digunakan untuk mengambil keputusan yang berkaitan dengan klasifikasi.
  3. Algoritma Clustering: Algoritma ini digunakan untuk mengelompokkan objek yang serupa seperti mengelompokkan pelanggan berdasarkan preferensi pembelian, atau mengelompokkan sampel data berdasarkan karakteristik. Algoritma ini digunakan untuk mengidentifikasi pola dan menemukan struktur dalam data.
  4. Deep Learning: Algoritma ini digunakan untuk menyelesaikan masalah yang sangat kompleks seperti pengenalan wajah, pengenalan suara, atau pengolahan bahasa alami. Algoritma ini digunakan untuk membuat sistem yang dapat belajar secara otomatis dan meningkatkan performanya dengan waktu.
  5. Algoritma Decision Tree: Algoritma ini digunakan untuk membuat suatu diagram pohon yang menyajikan keputusan berdasarkan kondisi-kondisi yang diberikan. Algoritma ini digunakan untuk mengambil keputusan yang berkaitan dengan klasifikasi atau regresi
  6. Algoritma Gradient Boosting: Algoritma ini digunakan untuk membuat sekumpulan model yang dapat digabungkan untuk memprediksi hasil. Algoritma ini digunakan untuk membuat model yang lebih kompleks dan akurat dibandingkan dengan menggunakan model tunggal.
  7. Algoritma Random Forest: Algoritma ini digunakan untuk membuat sekumpulan decision tree yang dapat digabungkan untuk memprediksi hasil. Algoritma ini digunakan untuk membuat model yang lebih kompleks dan akurat dibandingkan dengan menggunakan model tunggal.
  8. Algoritma Neural Network : Algoritma ini digunakan untuk menyelesaikan  masalah yang kompleks seperti pengenalan wajah, pengenalan suara, atau pengolahan bahasa alami. Algoritma ini digunakan untuk membuat sistem yang dapat belajar secara otomatis dan meningkatkan performanya dengan waktu. Neural network dapat digunakan untuk pemrosesan gambar, teks, suara dan video. Neural network juga dapat digunakan untuk tugas-tugas yang memerlukan pembelajaran dari data yang tidak terstruktur.
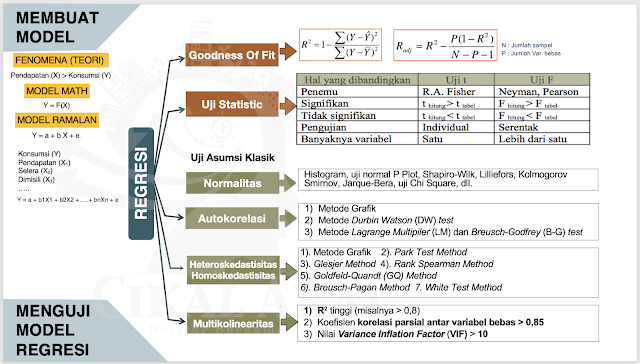
Berikut Tipe Machine Learning, Variabel target dan Algoritma yang digunakan.

Regresi yang Baik untuk Prediksi

Secara visual regresi yang baik memenuhi asumsi Statistik dan Asumsi Klasik sebagaimana dirangkum pada gambar berikut:


Hal terpenting yang perlu diperhatikan sebelum memilih model analisa regresi adalah memperhatikan tipe data atau tipe variabel target (Tipe Dependen Variabel) yang digunakan. Secara visual dapat dilihat pada gambar berikut:
Referensi:
https://www.alamyin.com/2023/05/analisa-tren-dengan-algoritma-regresi.html
https://devopedia.org/types-of-regression
https://www.analyticsvidhya.com/blog/2022/01/different-types-of-regression-models/
https://medium.com/@codekalimi/list-of-machine-learning-models-61b51ad492f1
https://www.researchgate.net/publication/336160040_Feature_selection_with_the_R_package_MXM/figures?lo=1

27/08/2023

Pemrograman Data Sains (1)

August 27, 2023  , , ,  No comments

Pemrograman Data Sains (1)

ADA banyak bahasa pemrograman untuk data sians. Dinataranya Python, R Matlab, Javasript, dll. Python menjadi salah satu bahasa pemrograman yang paling populer karena tak hanya dibutuhkan untuk bidang data science, tapi juga berguna untuk pengembangan web dan software. Bahasa pemrograman ini termasuk object-oriented programming. Dalam data science, Python umumnya digunakan untuk pemrosesan data dan penerapan algoritma analisis data. Python juga sangat mudah dipelajari oleh data scientist atau programmer pemula karena menggunakan sintaks yang sederhana.

Berikut adalah Tahapan Data Sains:

Data science adalah ilmu yang menggabungkan matematika, statisika dengan ilmu komputer dengan tujuan analisa data (data analysis) dari suatu himpunan data baik skala kecil (sampel) maupun besar (populasi) dengan mengaplikasikan algoritma tertentu untuk tujuan menggali data (data mining) dan mendapatkan pola data serta dapat melakukan prediksi data (prediction) dengan cukup akurat yang dapat membantu dalam pengambilan keputusan dan dapat digunakan untuk membuat sistem yang cerdas (AI) yang dapat terus belajar dengan sendirinya (machine learning). 

Berikut adalah materi Pengantar Pemrograman Data Sains

  • Pengertian Data Sains 
  • Tujuan data science 
  • Jenis pembelajaran data science 
  • Tahapan data sains 
    • Pertama, tahap pendefinisian masalah. 
    • Kedua, tahap pengumpulan data. 
    • Ketiga, tahap eksplorasi dan penyiapan data. 
    • Keempat, tahap analisis data. 
    • Kelima, storytelling. 
  • Keahlian dan skill data scientist 
  • Perbedaan data sains (machine learning) dengan pemrograman tradisional ? 
  • Mengapa python?

SIlakan dibaca materi lengkapnya Pengantar Data Sains Namun sebaiknya membaca juga materi Statistik dan data sains dan pengantar algoritma pemrograman 

Dalam Mata Kuliah ini materi dna praktik yang akan dipelajari

TOPIK PEMROGRAMAN DATA SAINS WITH PYTHON 

  1. Pengantar Paket dan Library Python untuk data sains 
  2. Numpy 
  3. Pandas 
  4. Matplotlib, Seaborn 
  5. Visualisasi Data 
  6. Machine Learning (Intro)
  7. Projek
















Selamat Belajar, Enjoy dan Merdekalah.

22/05/2023

ANALISA TREN DENGAN ALGORITMA REGRESI

May 22, 2023  , , ,  No comments

 ANALISA TREN

Dalam metode statistik ini, ada tiga jenis data yang bisa digunakan dalam analisis, yaitu data cross section, data time series, dan data panel (gabungan cross section dan time series).

Data time series adalah jenis data berdasarkan waktu yang memiliki banyak titik waktu. Banyak titik waktu di sini berarti waktunya lebih dari satu periode waktu. Berbeda dengan data cross section/silang waktu yang periode waktunya hanya 1 titik waktu. Periode waktu bisa 1 detik, 1 meni, 1 jam, 1 hari, 1 minggu, 1 bulan, 1 dekade, 1 tahun, 1 abad, dan seteresunya. Misalnya, dalam kurun waktu 1 tahun (data cross section), terdiri 12 bulan (data time series).

Tren adalah pergerakan jangka panjang dalam suatu kurun waktu yang kadang-kadang dapat digambarkan dengan garis lurus atau kurva mulus. Analisis trend digunakan untuk membangun model umum kecenderungan data berkala (time series) untuk keperluan peramalan (proyeksi tren). Analisis trend dipakai untuk data dengan horison waktu yang lama (sebaiknya lebih dari 10 tahun) dan tidak mengandung komponen musiman.

Beberapa model analisis yang umum dipakai :

  • Linier dan non linier (2-4)
  • Kuadratik 
  • Eksponensial
  • Kurva-S

Perhatikan Ilustrasi Berikut
















Gambar1 : Pola Time Series

Dalam analisa tren ada beberapa istilah:
  • Tren jangka panjang adalah suatu garis (trend) yang menunjukkan arah perkembangan secara umum.
  • Variasi musim adalah suatu gerakan yang naik turun secara teratur yang cenderung untuk terulang kembali dalam jangka waktu tidak lebih dari 1 tahun.
  • Variasi siklis adalah suatu gerakan yang naik turun secara teratur yang cenderung untuk terulang kembali setelah jangka waktu lebih dari 1 tahun.
  • Variasi random adalah suatu gerakan yang naik turun secara tiba-tiba atau mempunyai sifat yang sporadis sehingga biasanya sulit untuk diperkirakan sebelumnya

Mengapa Analisa Tren Penting?

Analisis tren memiliki beberapa kepentingan yang menjadikannya penting dalam berbagai bidang. Berikut adalah beberapa alasan mengapa analisis tren penting:
  1. Mengidentifikasi Pola dan Perubahan: Analisis tren membantu mengidentifikasi pola perubahan dalam data seiring waktu. Ini dapat membantu dalam memahami arah dan kecenderungan data serta mengidentifikasi apakah ada perubahan signifikan atau pola yang konsisten.
  2. Prediksi dan Perencanaan: Dengan memahami tren masa lalu, analisis tren dapat digunakan untuk membuat prediksi tentang masa depan. Informasi tren yang dihasilkan dapat membantu dalam perencanaan strategis, pengambilan keputusan, dan peramalan, sehingga membantu mengurangi ketidakpastian dan meningkatkan efisiensi.
  3. Evaluasi Kinerja: Analisis tren dapat digunakan untuk mengevaluasi kinerja suatu variabel atau fenomena seiring waktu. Misalnya, dalam bisnis, analisis tren dapat membantu dalam melihat pertumbuhan penjualan, laba, atau pengeluaran dan membandingkannya dengan target atau periode sebelumnya.
  4. Deteksi Anomali: Dengan memahami tren yang normal, analisis tren dapat membantu dalam mendeteksi anomali atau perubahan yang tidak biasa dalam data. Hal ini dapat membantu dalam mengidentifikasi masalah atau kesalahan yang mungkin terjadi dan mengambil tindakan yang sesuai.
  5. Pengambilan Keputusan: Analisis tren memberikan wawasan yang berharga dalam tren jangka panjang dan memungkinkan pengambilan keputusan yang lebih informasi. Informasi tren dapat membantu dalam mengidentifikasi peluang, mengelola risiko, dan mengoptimalkan strategi bisnis atau kebijakan publik.

Perhatikan tren IHSG berikut















Gambar 2: Ilustrasi tren IHSG


Berikut perbedaan tren linier dan non linier

1. Analisis Tren Linier:
Analisis tren linier melibatkan penggunaan garis lurus untuk menggambarkan tren atau pola dalam data seiring waktu. Metode yang umum digunakan dalam analisis tren linier adalah regresi linier, di mana garis lurus terbaik ditempatkan di antara titik-titik data untuk memperkirakan hubungan linier antara variabel dependen (y) dan variabel independen (x). Jika garis tersebut memiliki kemiringan positif, itu menunjukkan tren naik, sedangkan kemiringan negatif menunjukkan tren menurun. 

2. Analisis Tren Nonlinier:
Analisis tren nonlinier mencoba untuk menggambarkan pola yang tidak dapat dijelaskan oleh garis lurus atau hubungan linier. Dalam analisis tren nonlinier, berbagai jenis fungsi matematika dan model statistik digunakan untuk memodelkan dan menggambarkan tren yang lebih kompleks. Beberapa metode analisis tren nonlinier yang umum meliputi regresi nonlinier, smoothing spline, regresi polinomial, dan model eksponensial. 


Gambar 3 : Ilustrasi Forecasting (peramalan)

Salah satu tujuan utama analisa tren adalah untuk melakukan peramalan/forecasting.
Peramalan (forecasting) merupakan suatu proses perkiraan keadaan pada masa yang akan datang dengan menggunakan data di masa lalu (Adam dan Ebert, 1982)











Gambar 4 : Ilustrasi Error

Analisis Tren Linier dengan Algoritma Regresi Linier

Regresi adalah metode statistika yang digunakan untuk memodelkan dan menganalisis hubungan antara satu atau lebih variabel independen (prediktor) dengan satu variabel dependen (yang ingin diprediksi). Tujuan utama dari regresi adalah untuk mengidentifikasi dan mengukur pengaruh variabel independen terhadap variabel dependen.

Secara umum, regresi dapat dibedakan menjadi dua jenis utama: regresi linier dan regresi non-linier. Regresi linier melibatkan hubungan linier antara variabel independen dan dependen, sementara regresi non-linier melibatkan hubungan yang lebih kompleks dan non-linier antara variabel tersebut.
Regresi linier sering digunakan dan merupakan salah satu bentuk yang paling umum dari analisis regresi. Dalam regresi linier, hubungan antara variabel independen dan variabel dependen dapat dijelaskan dengan persamaan garis lurus. Regresi linier memodelkan hubungan ini dengan mengestimasi koefisien regresi yang menggambarkan sejauh mana perubahan dalam variabel independen akan mempengaruhi perubahan dalam variabel dependen.


Penggunaan algoritma regresi Linier maupun non linier paling banyak digunakan dan kerap keliru diterapkan pada saat melakukan interpretasi model regresi.















Gambar 5: Ilustrasi Membuat dan menguji Model Regresi


Penjelasan Lengkap di Modul Cikal Akal. Analisa Tren dan Machine Learning.


Memaknai model Regresi dengan Bijak


Misalnya kita mempunyai dua model persamaan Linier antara 2 entitas. 
X adalah variabel bebas, Pendapatan
Y adalah variabel terikan, Konsumsi

Model 1. Y =  3X +3
Model 2. Y =  9x + 3

Perhatikan Ilustrasi Berikut















Gambar 6: perbandingan dua model Linier

Dalam penerapan statistik dan matematika dalam ekonomi, ada 3 model penjelasan untuk menjelasakan dan menafsirkan model.

Bagaimana Anda menafsirkan model regresi ini dengan bijak dan bermakna?

Model 1. Y =  3X +3
Model 2. Y =  9x + 3
Silakan dijelaskan dengan:
  1. Narasi
  2. Tabel
  3. Gambar / Kurva
Sesuai selera Anda, dan bisa Anda pahami dengan baik.

Contoh Kasus Regresi Berganda. 1 variabel dependen, dan dua variabel bebas.
X1: Pengeluaran Makanan (Rp10.000) 
X2: Pengeluaran Transportasi (Rp.10.000)
X3: Berat Badan (kg) (Y)

No.  X1.  X2.    Y
1 50 20 60
2 40 25 55
3 60 30 65
4 55 35 70
5 45 40 62
6 65 50 75
7 70 55 80
8 75 60 85
9 80 65 90
10 90 70 95

Untuk memperoleh model regresi dari data di atas dapat dilakukan dengan 3 cara
  1. Cara Manual Eliminasi dan subtitusi persamaan
  2. Menggunakan aplikasi pengolah data seperti excel, evies, SPSS, STATA, dll
  3. Menggunakan bahasa pemrograman (koding)
Berdasarkan data di atas, peneliti ingin membangun model regresi untuk memprediksi berat badan (Y) berdasarkan pengeluaran makanan (X1) dan pengeluaran transportasi (X2).

Tugas Kita adalah melakukan analisis regresi dengan menggunakan data di atas untuk menentukan persamaan regresi (model ramalan) dan koefisien regresi yang sesuai.

Untuk menghasilkan persamaan regresi dan koefisien regresi menggunakan Excel, Kita dapat mengikuti langkah-langkah berikut:

  1. Masukkan data yang diberikan ke dalam spreadsheet Excel. Misalnya, Kita dapat menempatkan data pada kolom A hingga D, dengan kolom A untuk nomor partisipan, kolom B untuk pengeluaran makanan (X1), kolom C untuk pengeluaran transportasi (X2), dan kolom D untuk berat badan (Y).
  2. Selanjutnya, pada sel E2, masukkan rumus regresi menggunakan fungsi "LINEST". Misalnya, rumusnya dapat dituliskan >>>>. =LINEST(D2:D11, B2:C11) Pastikan untuk menyesuaikan rentang sel dengan data yang tepat.
  3. Tekan kombinasi tombol Ctrl + Shift + Enter untuk mengkonfirmasi rumus sebagai rumus matriks. Dalam beberapa versi Excel, Kita mungkin perlu menekan Enter setelah memasukkan rumus.
  4. Setelah itu, Excel akan menghasilkan output matriks dalam rentang sel E2:F3. Sel E2 akan berisi koefisien regresi (intersep dan koefisien X1), sedangkan sel F2 akan berisi koefisien X2.
  5. Untuk menampilkan persamaan regresi berdasarkan koefisien yang dihasilkan, Kita dapat memasukkan rumus berikut di sel G2="Y = "&E2&" + "&F2&" * X1 + "&G2&" * X2"
Ini akan menghasilkan persamaan regresi dengan koefisien yang sesuai.

Kode Python

Kode Python untuk menganalisis data regresi dengan 2 variabel bebas dan 1 variabel terikat menggunakan paket statsmodels:

#Import Library
import numpy as np
import pKitas as pd
import statsmodels.api as sm

# Membuat DataFrame dari data yang diberikan
data = {
    'Partisipan': np.arange(1, 11),
    'Peng Makanan': [50, 40, 60, 55, 45, 65, 70, 75, 80, 90],
    'Peng Transportasi': [20, 25, 30, 35, 40, 50, 55, 60, 65, 70],
    'Berat Badan': [60, 55, 65, 70, 62, 75, 80, 85, 90, 95]}

df = pd.DataFrame(data)

# Memisahkan variabel independen dan dependen
X = df[['Pengeluaran Makanan', 'Pengeluaran Transportasi']]
y = df['Berat Badan']

# Menambahkan kolom konstanta untuk intercept
X = sm.add_constant(X)

# Membangun model regresi
model = sm.OLS(y, X)
results = model.fit()

# Menampilkan hasil
print(results.summary())

Silakan Tampilkan Outputnya dan Lakukan uji Model sesabgaimana Gambaran pada Gambar 5 di atas.

Diskusi dan pendalaman di kelas offline / online.

Salam Hangat, MATH IS GREAT :D